Modellierung stochastischer Situationen[1]

PDF-Datei

1.      Begriff der stochastischen Situation

Die Bereiche der Realität, die Gegenstand der Wissenschaft Stochastik in unserem Sinne sind, bezeichnen wir nach einem Vorschlag von Schupp (1984) als stochastische Situationen. Unter einer stochastischen Situation verstehen wir zum einen Situationen in der Realität, in denen Daten entstehen und erfasst werden können, und zum anderen Situationen, in denen verschiedene Ergebnisse möglich sind, aber nicht mit Sicherheit feststeht, welches eintreten wird. Mit dem Begriff der stochastischen Situation wollen wir alle Anwendungsbereiche einer Stochastik in unserem Sinne erfassen.

Das Wort „Situation“ hat in der Umgangssprache im Wesentlichen zwei Bedeutungen (Kunkel-Razum et al. 2003, S. 1458). Es bezeichnet zum einen Verhältnisse und Umstände, in denen sich jemand augenblicklich befindet, wie es etwa in den Redewendungen eine gefährliche Situation, eine Situation meistern oder in eine Situation bringen zum Ausdruck kommt. Es geht also in der Regel um eine zeitlich begrenzte, aktuelle Lage, in der sich eine Person unmittelbar befindet. Zum anderen werden mit „Situation“ aber auch ein allgemeiner Zustand bzw. allgemeine Verhältnisse bezeichnet, wie zum Beispiel die wirtschaftliche Situation in einem Land. Stochastische Situationen können beide Bedeutungen beinhalten. So haben zum Beispiel der Weitsprung eines Schülers oder Glücksspiele einen situativen, also zeitlich begrenzten Charakter. Stochastische Situationen in der zweiten Bedeutung liegen etwa bei Überlegungen zum Wetter (die Wetterlage) vor.

Anstelle von stochastischen Situationen wird auch von „Erscheinungen mit Zufallscharakter“ oder von „zufälligen Erscheinungen“ gesprochen. Gegen die Verwendung dieser Bezeichnung spricht, dass sie aufgrund der Verwendung des Zufallsbegriffs in der Mathematik in eingeschränkter Weise oft nur mit Situationen verbunden, bei denen gleichwahrscheinliche Ergebnisse auftreten, wie etwa bei vielen Glücksspielen.

Stochastische Situationen finden sich in allen Bereichen von Natur und Gesellschaft.

• Beispiele aus der Natur sind die Wetterentstehung, das Pflanzenwachstum oder die körperliche Entwicklung von Menschen und Tieren.
• In der Technik gibt es stochastische Situationen im Bereich von Produktions- und Transportprozessen.
• Im persönlichen Leben eines jeden Menschen handelt es sich bei der Entwicklung von Freizeitinteressen, Kenntnissen, Fähigkeiten und Einstellungen um stochastische Situationen. Aber auch alltägliche Vorgänge wie das Schlafen, Frühstück essen, zur Schule gehen, Spielen, Hausaufgaben erledigen u. a. haben in der Regel einen stochastischen Charakter bezüglich bestimmter Merkmale.
• Typische stochastische Situationen gibt es beim Werfen von Münzen oder Würfeln, Drehen von Glücksrädern, Ziehen aus einem Behältnis, Lotto spielen u. a.
• Bei Forschungsarbeiten auf den Gebieten der Soziologie, Psychologie, Pädagogik oder Medizin stehen Wissenschaftler oft vor der stochastischen Situation, Schlussfolgerungen aus Daten ableiten zu müssen.

Allen stochastischen Situationen ist gemeinsam, dass es Unsicherheiten über die möglichen Ergebnisse etwa der Entwicklung des Wetters, der Aneignung von Kenntnissen durch einen Schüler oder der Überlegungen eines Wissenschaftlers gibt. Es ist prinzipiell unmöglich vorherzusagen, welches Ergebnis eintreten wird. Mit den Mitteln der Stochastik können diese Unsicherheiten aber quantifiziert werden. Auf dieser Grundlage lassen sich im Zusammenhang mit anderen Informationen begründete Entscheidungen treffen. Stochastik wird deshalb auch als das Treffen begründeter Entscheidungen im Falle von Unsicherheit bezeichnet. An dieser Stelle sei darauf hingewiesen, dass „stochastisch“ und „Stochastik“ teilweise synonym für wahrscheinlichkeitstheoretisch und Wahrscheinlichkeitsrechnung (oft zusammen mit mathematischer Statistik) gebraucht werden. Diese Auffassungen basieren auf dem ursprünglichen Gebrauch der Wörter in der Mathematik (Huber 2015) und sind auch in der fachdidaktischen Literatur vorhanden (Büchter und Henn 2007). 

2.      Modellierung stochastischer Situationen

Mit dem Begriff der stochastischen Situation wird zunächst nur eine äußere Erscheinung erfasst, deren stochastischer Charakter im Rahmen eines Modellierungsprozesses analysiert werden muss.

Bei der Modellierung stochastischer Situationen werden drei verschiedene Ebenen unterschieden, deren Zusammenwirken in der Fehler! Verweisquelle konnte nicht gefunden werden. veranschaulicht wird:

• die Ebene der realen Erscheinungen und Zustände (Realität),
• die Ebene der Realmodelle und
• die Ebene der theoretischen Modelle (Theorie).

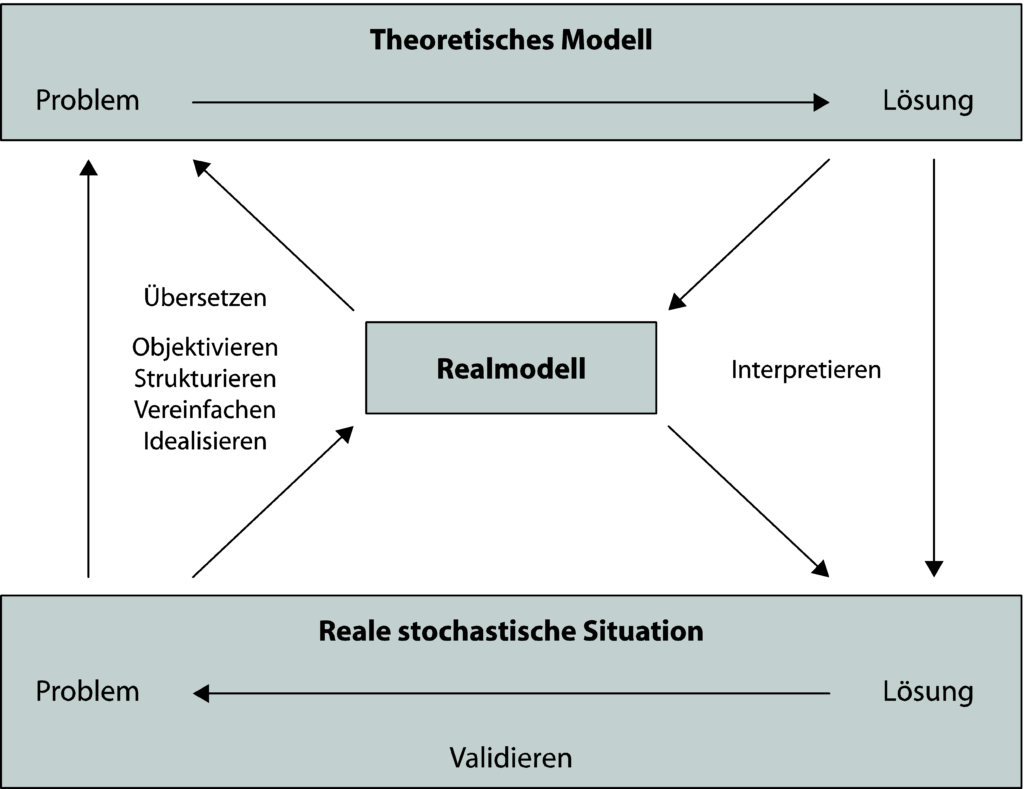
Abb.1 Schematische Darstellung der Modellierung stochastischer Situationen. (Aus Krüger et al. 2015, S. 13; mit freundlicher Genehmigung von Springer-Verlag GmbH Deutschland.)

Im Folgenden soll die Modellierung stochastischer Situationen an zwei Beispielen erläutert werden: dem Schreiben einer Mathematikarbeit und dem Werfen eines Würfels.

Für die stochastische Situation des Schreibens einer Mathematikarbeit durch den Schüler Arne können die drei Ebenen in folgender Weise beschrieben werden.

• Realität: Arne löst in 45 min die vorgegebenen Aufgaben in einer Klassenarbeit. Als Ergebnis liegt die konkrete Arbeit von Arne mit seinen Antworten vor. Er kann aber auch wegen einer Erkrankung die Arbeit vorzeitig beenden oder die Leistung generell verweigern. Die Arbeit hat eine Reihe real existierender Eigenschaften wie die Art der Antworten, die Lesbarkeit, vorgenommenen Korrekturen, weitere Bemerkungen oder Zeichnungen von Arne u. a.
• Realmodell: Bei der Korrektur der Arbeit durch die Lehrkraft wird als Merkmal nur die Richtigkeit der Antworten betrachtet. Dazu muss die Lehrkraft zunächst einen Bewertungsmaßstab festlegen. Sie ordnet den zu erwartenden Teilleistungen Punkte zu. Weiterhin muss sie eine Reihe von vereinfachenden Annahmen machen. So wird sie den aktuellen Gesundheitszustand und die Leistungsbereitschaft des Schülers nicht berücksichtigen. Wenn Arne nicht alle Teilschritte notiert hat, kann sie annehmen, dass er diese trotzdem durchdacht hat u.a.m.
• Theorie: Bei der Entwicklung und Auswertung von zentralen Vergleichsarbeiten, wie zum Beispiel VERA 3, wird zur Beschreibung der Leistungen der Schüler das Rasch-Modell verwendet, das nach dem dänischen Statistiker Georg William Rasch (1901–1980) benannt ist. Dabei wird vereinfachend angenommen, dass es eine eindimensionale mathematische Fähigkeit gibt, die mit der gleichen Skala wie die Schwierigkeit der Aufgaben gemessen werden kann. Dieser Fähigkeit wird dann für jede Aufgabe eine Lösungswahrscheinlichkeit zugeordnet. Im Ergebnis der Auswertung erhält man für einen Schüler keine Erfüllungsquoten sondern nur eine Einordnung der Leistung in Kompetenzstufen.

Für den im Unterricht häufig als Standardbeispiel einer stochastischen Situation verwendeten Vorgang des Werfens eines Spielwürfels durch eine Person führt die Modellierung zu folgenden Ergebnissen.

• Realität: Nach dem Werfen des Spielwürfels auf einem Tisch kann der Würfel von Tisch heruntergefallen sein und auf dem Boden liegen, er kann „auf Kippe“, auf einer Ecke (z. B. bei einer genoppten Tischdecke) oder auf einer bestimmten Stelle auf dem Tisch auf einer Seitenfläche liegen bleiben. Als Merkmale des eingetretenen Ergebnisses könnte der Abstand zur Tischkante, der Winkel der Seitenflächen zum Tisch oder die Punktzahl auf der oben liegenden Seite gewählt werden. Ein realer Spielwürfel ist nicht völlig homogen aufgebaut, alleine schon durch die Vertiefungen für die Augenzahlen oder Abrundungen der Ecken. In Spielcasinos werden speziell angefertigte Würfel verwendet, die dem Ideal eines homogenen Würfels möglichst nahe kommen. Einen (realen) Spielwürfel bezeichnen wir allgemein als ein Glücksspielgerät.
• Realmodell: Bei Schüleraufgaben zum Würfeln mit einem normalen Spielwürfel werden meist ohne explizite Nennung folgende Modellannahmen getroffen: Der Würfel fällt nicht vom Tisch und es wird auf einer glatten Unterlage gewürfelt, so dass der Würfel auf einer Seite zu liegen kommt und immer eine Augenzahl oben liegt. Weiterhin wird angenommen, dass alle sechs möglichen Ergebnisse gleichwahrscheinlich sind, wodurch Berechnungen von Wahrscheinlichkeiten erfolgen können.
• Theorie: Auf der theoretischen Ebene wird von einem Würfel im mathematischen Sinne (als gedankliches Objekt) ausgegangen, bei dem jeder der sechs Seiten genau einer der Zahlen 1 bis 6 zugeordnet ist. Das „Würfeln“ wird in folgender Weise beschrieben: Auf der Ergebnismenge: E = {1, 2, 3, 4, 5, 6} ist mit P(k) = 1/6 , k ∈ E eine Wahrscheinlichkeitsverteilung definiert. Der mathematische Würfel mit den zugeordneten Zahlen heißt auch idealer Würfel oder Laplace-Würfel und allgemein kann er als Zufallsgerät bezeichnet werden. Dieses theoretische Würfeln ist ein Beispiel für den theoretischen Begriff Zufallsexperiment. In dem theoretischen Modell kann dann die Wahrscheinlichkeit eines Ereignisses (als Teilmenge der Ergebnismenge) berechnet werden. Weiterhin kann mit einem Test überprüft werden, ob die Daten aus einem realen Experiment mit einem realen Spielwürfel mit dem theoretischen Modell des Zufallsexperimentes verträglich sind.

Diese drei Ebenen werden in der Literatur und auch in Unterrichtsmaterialien oft nicht auseinandergehalten. Das führt dann zu Begriffsverwirrungen oder auch dazu, dass in Unterrichtsvorschlägen für die Primarstufe bereits ein Arbeiten auf der Ebene der theoretischen Modelle erfolgt. So werden in den aktuellen Bildungsstandards für die Primarstufe die Begriffe Ereignis und Zufallsexperiment verwendet, die zur Ebene der theoretischen Modelle gehören. Wir halten es weder für sinnvoll noch für notwendig, bereits in der Primastufe bis zur Ebene der theoretischen Modelle vorzudringen.

3.      Prozessbetrachtung stochastischer Situationen

Es gibt verschiedene Möglichkeiten, stochastische Situationen systematisch zu untersuchen. Eine davon ist die Methode der Prozessbetrachtung, die insbesondere an der Universität Rostock entwickelt, im Unterricht der Primarstufe und Sekundarstufe I erprobt und in Materialien für Schülerinnen und Schüler umgesetzt wurde. Diese Methode gestattet es, den oft unverbundenen Umgang mit statistischen Daten und Aufgabenstellungen zur Wahrscheinlichkeitsrechnung in einer einheitlichen begrifflichen Weise zu beschreiben. Weiterhin ist ein enger Lebensweltbezug möglich. Das Besondere der Prozessbetrachtung ist, dass nicht nur das betrachtet wird, was eingetreten ist, sondern auch der Prozess untersucht wird, in dessen Resultat diese Ergebnisse eintreten können.

Das zentrale Modellierungsmittel ist der Begriff stochastischer Vorgang und die damit im Zusammenhang stehenden Betrachtungsweisen. Ein stochastischer Vorgang ist ein Realmodell für einen tatsächlichen Vorgang in der Natur, der Gesellschaft oder dem Denken. Das einzige definierende Merkmal eines solchen Vorgangs ist die Existenz mehrerer möglicher Ergebnisse.

Auf das Adjektiv „stochastisch“ sollte in der Primarstufe verzichtet werden und auch das Wort „Vorgang“ braucht im Unterricht nur selten benutzt zu werden. Wir empfehlen, den tatsächlichen Vorgang konkret zu benennen (Weitsprung eines Schülers, Wachstum einer Blume, Werfen eines Würfels). Als allgemeine Bezeichnung ist es ausreichend, von einem Vorgang mit mehreren möglichen Ergebnissen zu sprechen.

3.1.   Aspekte des Begriffs „Vorgang“

Zu den Aspekten des Begriffs „Vorgang“, gehören Gedanken, die an vier Beispielen erläutert werden sollen. Die Beispiele A und B betreffen das Arbeiten mit Daten und die Beispiele C und D das Arbeiten mit Wahrscheinlichkeiten.

Beispiele:

1. Arne schreibt eine Mathematikarbeit.
2. Ein Baum wächst im Wald.
3. Cornelius würfelt.
4. Dilara überlegt, ob sie in der Arbeit die Aufgaben richtig gelöst hat.

Merkmale des Begriffs „Vorgang“

• Vorgänge treten in allen Bereichen des Lebens auf.
• Jeder Vorgang hat einen Anfang und ein Ende.
• Es können Vorgänge betrachtet werden, die schon abgeschlossen sind (Arne hat die Arbeit geschrieben.), die noch andauern (das Wachstum des Baumes) oder noch bevorstehen (der nächste Wurf von Cornelius).
• Es gibt Vorgänge, die sehr kurz sind (Würfeln), die etwas länger dauern (Schreiben einer Arbeit) und die sehr lange dauern (Wachstum eines Baumes).
• Es gibt Vorgänge, deren Ergebnis Personen nicht beeinflussen (Würfeln), und Vorgänge, bei denen die beteiligten Personen das Ergebnis beeinflussen können (Schreiben einer Mathematikarbeit).
• Es muss unterschieden werden zwischen dem, was abläuft und dem, was nach dem Ablauf eines Vorgangs eintreten kann (Tab. 1).

Tab. 1 Beispiele zum Ablauf und zu möglichen Ergebnissen von Vorgängen

3.2.   Bestandteile einer Prozessbetrachtung

Bestimmung eines einzelnen Vorgangs, der beteiligten Personen oder Objekte und der Resultate des Vorgangs

In den Formulierungen der obigen vier Beispiele sind die Vorgänge sowie die beteiligten Personen oder Objekte bereits genannt. Dies ist aber bei Aufgabenstellungen in der Stochastik oft nicht der Fall. Insbesondere, wenn es um das Arbeiten mit Daten geht, werden meist nur die jeweiligen konkreten Daten genannt, wie zum Beispiel die Ergebnisse einer Befragung zu den Lieblingstieren von Kindern. In diesen Fällen kann überlegt werden, im Ergebnis welchen Vorgangs die Daten entstanden sind. Auch bei Aufgaben zu Wahrscheinlichkeiten kann dieses Problem auftreten, wenn es in Aufgabenstellungen bereits um die Wiederholung eines Vorgangs geht, bzw. wenn ein Vorgang aus mehreren Teilvorgängen besteht, wie zum Beispiel beim Werfen mit zwei Würfeln.

Nach dem Ablauf des Vorgangs sind bestimmte Resultate eingetreten (der Würfel liegt in einer bestimmten Lage auf dem Tisch), haben sich bestimmte Eigenschaften von Objekten oder von Personen herausgebildet, sind neue Objekte entstanden (die Arbeit von Arne) oder haben sich Gedanken im Kopf eines Menschen gebildet (die Vermutungen von Dilara zur Richtigkeit ihrer Lösungen).

Diese Dinge existieren alle auf der Realebene (der Wirklichkeit) und sind unabhängig von Betrachtungen eines Menschen. Ein Baum wächst, auch ohne dass dies näher betrachtet oder untersucht wird.

Nach der Bestimmung des zu untersuchenden Vorgangs beginnt ein schrittweiser Prozess der Modellierung der Wirklichkeit.

Bestimmung eines zu betrachtenden Merkmals

Die nach Ablauf des Vorgangs entstandenen Zustände, Eigenschaften, Objekte oder Gedanken besitzen zahlreiche Merkmale. Man sagt auch, sie sind Träger von Merkmalen bzw. Merkmalsträger. Wenn der Vorgang mit Mitteln der Statistik oder der Wahrscheinlichkeitsrechnung näher untersucht werden soll, muss man sich zunächst entscheiden, welches Merkmal man betrachten will (Tab. 2).

Tab. 2 Beispiele zu Resultaten und interessierenden Merkmalen

Festlegung des Messverfahrens zur Bestimmung der Ausprägungen des Merkmals und Ermittlung der Ergebnisse

Nachdem ein interessierendes Merkmal des Vorgangs ausgewählt wurde, muss überlegt werden, wie die konkreten Ausprägungen (die Werte) des Merkmals bestimmt werden können. Dazu werden Geräte, Skalen oder Methoden zum Messen benötigt. Manchmal ist es möglich, für ein Merkmal unterschiedliche Skalen zum Messen zu verwenden (Tab. 3).

Tab. 3 Beispiele zur Messung von Merkmalsausprägungen

Nachdem die Messskala bzw. die Messmethode festgelegt wurden, können nun damit die konkreten Ausprägungen des Merkmals gemessen werden. Wir bezeichnen die dabei ermittelten Merkmalsausprägungen als Ergebnisse des Vorgangs. Bei statistischen Untersuchungen spricht man von Daten.

Bestimmung der Bedingungen des Vorgangs

Wenn man die gemessenen Werte des Merkmals (z. B. die ermittelten Daten) oder die Wahrscheinlichkeiten der möglichen Ergebnisse hinterfragen oder einschätzen will, müssen die Bedingungen betrachtet werden, die Einfluss auf den Vorgang haben. Man spricht anstelle von Bedingungen auch von Einflussfaktoren (Tab. 4).

Tab. 4 Beispiele zu Bedingungen des Vorgangs

Die Bedingungen eines Vorganges können auf zwei verschiedenen Ebenen betrachtet werden, zum einen auf einer allgemeinen Ebene und zum anderen für einen konkreten Verlauf des Vorgangs. Das Wachstum eines Baumes wird z. B. durch allgemeine Bedingungen, wie den Nährstoffgehalt des Bodens, die Wasser- und Windverhältnisse oder die Baumsorte beeinflusst. Bei einem konkreten Baum an einem konkreten Standort müssen die Ausprägungen dieser Bedingungen betrachtet werden. Diese Ausprägungen sind die Ursachen für die Beschaffenheit des Baumes.

Mit der Einbeziehung von Bedingungen in die Prozessbetrachtung entstehen enge Bezüge zu den Betrachtungen von Gesetzen in den Naturwissenschaften, die auch stets nur unter bestimmten Bedingungen gelten.

Betrachtung von Wiederholungen des Vorgangs

In der Statistik und in der Wahrscheinlichkeitsrechnung spielen Massenerscheinungen und zahlreiche Wiederholungen eines Vorgangs eine wichtige Rolle. Ein wesentliches Ziel der Beschreibenden Statistik ist die Aufbereitung von Massendaten und in der Wahrscheinlichkeitsrechnung ist das Gesetz der großen Zahlen ein fundamentaler Zusammenhang.

Bei einer Prozessbetrachtung wird dagegen zunächst immer nur ein einzelner Vorgang in der bisher beschriebenen Weise untersucht. Die Wiederholbarkeit eines Vorgangs unter gleichen Bedingungen ist im Unterschied zum Begriff Zufallsexperiment in der Wahrscheinlichkeitsrechnung keine definierende Eigenschaft eines Vorgangs. Damit werden auch Vorgänge wie der Ablauf eines Fußballspiels oder die Gedanken eines Schülers zu seiner geschriebenen Arbeit als stochastische Situationen angesehen.

Ob ein Vorgang wiederholt abläuft, ob mehrere Vorgänge parallel verlaufen oder ob Vorgänge überhaupt zusammengefasst werden können, wird von uns als ein extra zu untersuchendes Problem angesehen. Eine Zusammenfassung von Vorgängen zu einer Gesamtheit ist nur sinnvoll, wenn wesentliche Bedingungen gleich bleiben oder mindestens vergleichbar sind (Tab. 5).

Tab. 5 Beispiele zu Wiederholungen des Vorgangs

3.3.   Stochastische und nichtstochastische Vorgänge

Bei einer Prozessbetrachtung können zwei verschiedene Fälle auftreten:

1. Ein Vorgang hat bezüglich eines Merkmals nur ein mögliches Ergebnis
2. Ein Vorgang hat bezüglich eines Merkmals mehrere mögliche Ergebnisse.

Dabei kann es sich durchaus um den gleichen Vorgang handeln (Tab. 6).

Tab. 6 Beispiele zur Anzahl der Ergebnisse eines Vorgangs

Der Fall, dass Vorgänge bezüglich eines Merkmals nur ein mögliches Ergebnis haben, kommt bei realen Erscheinungen sehr selten vor. Vorgänge in der Natur, der Gesellschaft und dem Leben eines Menschen haben in der Regel bezüglich der meisten Merkmale mehrere mögliche Ergebnisse. Wie lange ein Kind schläft, wie lange es die Zähne putzt, was es zum Frühstück isst, wie lange es zur Schule braucht, wen es dabei trifft, welche Zensur es in der Mathearbeit bekommt, mit wem es wie lange am Nachmittag spielt und wann es einschläft sind alles Merkmale beim Ablauf eines Tages, die viele mögliche Ergebnisse haben.

Der stochastische Charakter eines Vorgangs kann nur bezüglich eines Merkmals angegeben werden. Vorgänge, die bezüglich eines Merkmals nur ein Ergebnis haben, bezeichnen wir als nichtstochastische Vorgänge bezüglich des betrachteten Merkmals.

3.4.   Prozessbetrachtung bei statistischen Untersuchungen

Die in den Beispielen A und B vorgestellte Prozessbetrachtung kann im Rahmen entsprechender statistischer Untersuchungen in der Primarstufe erfolgen (Tab. 7).

Tab. 7 Beispiele zu statistischen Untersuchungen zu Vorgängen

Bei statistischen Untersuchungen geht es generell um die Erfassung von Ergebnissen bei einer großen Zahl von Vorgängen die meist gleichzeitig ablaufen und auch nach der Erfassung der Daten weiterlaufen.

Um Daten bewerten zu können, müssen die Bedingungen, unter denen sie entstanden sind, bekannt sein. Dies wird beim Umgang mit Daten im Alltag, in der Presse und auch in der Wissenschaft oft nicht beachtet. So können etwa die Ergebnisse einer Schülerbefragung zum Kinobesuch nur zutreffend bewertet werden, wenn man die konkreten Bedingungen in den Orten kennt, in denen die Befragung durchgeführt wurde.

Literaturverzeichnis

Büchter, Andreas; Henn, Hans-Wolfgang (2007): Elementare Stochastik. Eine Einführung in die Mathematik der Daten und des Zufalls. Zweite, überarbeitete und erweiterte Auflage. Berlin, Heidelberg: Springer-Verlag Berlin Heidelberg (Mathematik für das Lehramt). Online verfügbar unter http://site.ebrary.com/lib/alltitles/docDetail.action?docID=10186904.

Huber, Peter J. (2015): Stochastik und Zufall. In: Stochastik in der Schule 35 (3), S. 20–23.

Krüger, Katja; Sill, Hans-Dieter; Sikora, Christine (2015): Didaktik der Stochastik in der Sekundarstufe I. Aufl. 2015. Berlin, Heidelberg: Springer Berlin Heidelberg (Mathematik Primarstufe und Sekundarstufe I + II).

Kunkel-Razum, Kathrin; Scholze-Stubenrecht, Werner; Wermke, Matthias; Auberle, Anette (Hg.) (2003): Duden, deutsches Universalwörterbuch. 5. überarbeitete Aufl. Mannheim: Dudenverlag.

Schupp, Hans (1984): Sinnvoller Stochastikunterricht in der Sekundarstufe I. In: mathematica didactica 7 (4), S. 233–243.

Sill, Hans-Dieter; Kurtzmann, Grit Susann (2019): Didaktik der Stochastik in der Primarstufe. Berlin: Springer Spektrum (Mathematik Primarstufe und Sekundarstufe I + II).

[1] Auszug aus Sill und Kurtzmann 2019, S. 18–27.